Toxic

Georgineer said:

I thought this sounded a bit familiar. It's On the Waterfront with Marlon Branflake. "You don't understand! I could've had class. I could've been a contender. I could've been somebody..."

I've looked at your spreadsheet snippets, which are meaningless without column headings, but I do notice that you are quoting lengths to an accuracy of 10 microinches, or one micrometre. Tell me Clim, how are you going to achieve that with hand-worked wood?

George

Click to expand...

+/- tolerance is allowed. When I worked in a machine shop that made scales for logging trucks we had a +/- of about 0.04 inches. And if things workout for me, with a shop to work in I could probably get things within +/- 0.01 inch. And with what I'm building, it is a prototype. And if it works, then this build along with 2 or 3 others I have done will probably wind up in a museum in Saxony, Germany. Johann Bessler (1680 - 1743) lived in the Republic of Saxony which today is Saxony, Germany.
As for the math, I'll be able to say that scientists made this a toxic subject for one simple reason, they say gravity has no energy. And since gravity has no energy, the
momentum/force that gravity generates in a falling mass/body cannot be conserved.
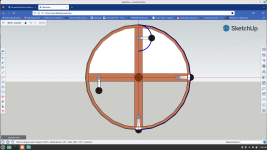
I've simplified the design in this drawing. When the weight passing top center is rotated 180º, the weight 90º after top center is the weight that is falling. If the weight is overbalanced by .25m then the top weight is being lifted .5m. This means that the weight 90º after top center needs to drop from .25m above the level of the axle to .25m below the level of the axle. And to rotate the weight passing top center will use only about 62% of the torque generated. I am building something using what Bessler called a "Peacock's Tail" so it will be somewhat authentic. The question is can the other 2 weights that are falling rotate the wheel? And at times all 4 overbalanced weights will generate torque/momentum. That's why I like this design.
With the spreadsheet, I'm not sure how many people use them. And if people don't use trigonometry to calculate torque then they wouldn't be familiar with the math.
I used 0º cosine to 90º Cosine and averaged it for the various frames of reference. Basically when is torque being generated and when does work being performed
decrease the amount of torque being generated. How I was able to calculate the net torque for what I'm building at about 9.3 in.lbs. of torque on average.
The radius of the wheel I'm building will be about 20" or 0.5m. This makes the "drop" of a weight about 1m. The average is 0.5m. Then if .5/9.81 = 0.05m/s.
Of course resistance would reduce that but then how much won't be known without it being built. Also the amount of overbalance might be able to be doubled.
Still, .04m/s with a 3.142 meter circumference translates to a little less than 1 rpm. I'm okay with that because this is impossible. And yet if it rotates more quickly than what math suggests then it will give a better understanding of how math applies to something like this.

What is the item?

Georgineer said:

I thought this sounded a bit familiar. It's On the Waterfront with Marlon Branflake. "You don't understand! I could've had class. I could've been a contender. I could've been somebody..."

I've looked at your spreadsheet snippets, which are meaningless without column headings, but I do notice that you are quoting lengths to an accuracy of 10 microinches, or one micrometre. Tell me Clim, how are you going to achieve that with hand-worked wood?

George

Click to expand...

Very carefully!

Newman109 said:

What is the item?

Click to expand...

"The solution to the World's Energy Problems!"

In Layman's terms, an attempt at Perpetual Motion.

It would be funnier, if it did not appear that the OP actually believes.

trevj said:

"The solution to the World's Energy Problems!"

In Layman's terms, an attempt at Perpetual Motion.

It would be funnier, if it did not appear that the OP actually believes.

Click to expand...

If this works it will be because I know how to calculate torque. I can calculate how much work it takes to lift a weight
using torque as well how much torque this design can generate. This is where if a person knows algebra and trigonometry
then this is something easy to factor. I've noticed no one has taken the time to consider the math.
And this works then I can point out what over 700 scientists at the IPCC don't understand about their own climate change
report. What is that worth? I think that'd be priceless. And I have this opportunity because they said that what I'm doing
isn't possible while I say Bessler's Wheel was built over 300 years ago. As for the science, I'll be introducing a new theory
that would allow for gasses to naturally occur in the atmosphere without the benefit of either the halogen or photolytic
processes.

Well, there's a lot of gas here, but it's of the laughing and flatulence nature...

Clim said:

If this works it will be because I know how to calculate torque. I can calculate how much work it takes to lift a weight
using torque as well how much torque this design can generate. This is where if a person knows algebra and trigonometry
then this is something easy to factor. I've noticed no one has taken the time to consider the math.
And this works then I can point out what over 700 scientists at the IPCC don't understand about their own climate change
report. What is that worth? I think that'd be priceless. And I have this opportunity because they said that what I'm doing
isn't possible while I say Bessler's Wheel was built over 300 years ago. As for the science, I'll be introducing a new theory
that would allow for gasses to naturally occur in the atmosphere without the benefit of either the halogen or photolytic
processes.

Click to expand...

No worries from over here. It won't work.

Not enough squirrels in it.

Milland said:

Well, there's a lot of gas here, but it's of the laughing and flatulence nature...

Click to expand...

I think some of the scientists whose research papers I cite might be interested in working with me. Scientists have said before
that a source of formaldehyde (CH2O) that could account for 40% of what their model requires would require a direct source.
My experiment if successful would demonstrate their missing formaldehyde while explaining how 3 greenhouse gasses are
associated with the recovery of the ozone layer.
And FYI, the IPCC's 2001 report stated that the warming between 1920 - 1945 was regional variance because it was in the northern
latitudes of the northern hemisphere. And that since 1978 is has been global.

See what my disabilities have brought into my life? The primary issue with working at Bessler's Wheel is that scientists said that momentum
cannot be conserved by an external force changing the motion of a body in motion. And yet that is an accepted definition of conserving
momentum. An example is what I am building. Tabs will contact a "stop" or bolt that goes across the frame. That resistance will be an external
force. The weights rotating downward will have more force than what it takes to rotate a weight when its tab has been kept from following its
path. This is where math has helped me to consider the work I do. The diagram shows 4 weights. The weight on the right by itself can rotate
the wheel while having the top weight rotate to be overbalanced. With 8 weights it should work better.
For anyone who wants to do the math, if the weight rotates 15 from the axle of the wheel, the CoG of the weight is a distance of 5 from where
it rotates. And if the top weight is lifted "10", then the wheel also rotates a distance of "10". The spreadsheet shows that the top weight being
rotted uses 62% of the overbalance the weight to the right generates while it is being lifted.
I have a lot of work to do so will relax and enjoy my build. If you don't have the time to go over the math, that's why I'm building, I took the time
to do the math. 2B nice I'll simplify the math. If the weight at the top is lifted "10", then it will drop "40". It will rotate around a different axis.
"40" is 4 x "10". This means that the overbalanced weight will use 3/4 of its force to rotate the wheel and 1/4 to rotate a weight to the
overbalanced position. And atmospheric chemistry is as easy as CO2 + H2O > CH2O + O2 then 2CH2O > CH4 + CO2. N2O occurs when O2 does
not make it into the ozone layer and instead 2N2O occurs.
2 B fair, with the science experiment if successful, it would show how atmospheric pressure, temperature, altitude and latitude, the position of the
Sun and the Van Allen radiation belts influence the rate at which said interactions occur. Without that information then it's just a guessing game. With
my builds, I took the time to do the math and then test the math. With my most recent build I am design my own roller bearings. If those bearings work
then my last build will probably work as well. It's the last photo. https://photos.app.goo.gl/8rQ7vSoWUqQZd83TA

"If he builds it, they will come."

This is a basic explanation. The blue lines for the weights shows their radii around their respective axis of rotation.
The overbalanced weight in this drawing is scaled 4:1 (radius of the overbalanced weight when compared to the top
weight). The overbalance radius is 20 inches. The weight at top being rotated has a radius of 5 inches. It will use 1/4
of the power the overbalanced weight generates for it's 180º of rotation.
As for the science, it'll likely be the same story. Once the interactions are known to occur then scientists will be more
willing to work with me. And yet because some scientists say that their models do not agree with the observed levels
of CH2O observed in the atmosphere might be interested in working with me. I'd be helping to showcase their research.
This basically means that if the build I am working on is successful then I'll most likely be doing woodworking and
scientific research at the same time. Is that even allowed or is it against the rules?

p.s., What I am building will be using 8 weights. This means that when the top weight is being rotated upwards that 2
other weights will be performing work as well. This is where if 16 weights were used then one weight could always be
rotating upwards. Then the average torque that 6 weights generate would be pretty much the constant torque the wheel
would be generating.

Clim said:

… 2B nice I'll simplify the math. If the weight at the top is lifted "10", then it will drop "40". It will rotate around a different axis.
"40" is 4 x "10". This means that the overbalanced weight will use 3/4 of its force to rotate the wheel and 1/4 to rotate a weight to the
overbalanced position. And atmospheric chemistry is as easy as CO2 + H2O > CH2O + O2 then 2CH2O > CH4 + CO2. N2O occurs when O2 does
not make it into the ozone layer and instead 2N2O occurs.
2 B fair, with the science experiment if successful, it would show how atmospheric pressure, temperature, altitude and latitude, the position of the
Sun and the Van Allen radiation belts influence the rate at which said interactions occur. Withoinformation then it's just a guessing game. With
my builds, I took the time to do the math and then test the math.

Click to expand...

No please, do show your math. Charlatans omit the proof.

It’s a total waste of a biochem degree to even respond to this, but your chemical nomenclature makes no sense. They’re not even equations. Atmospheric chemistry is not “as easy as” that garbage you’ve posted.

Why is this site allowing such trash to be proliferated, and worse, documented? It’s an insult to those who have rigorously studied for years and spent tens of thousands of dollars to obtain credentials in science and engineering.

RC Mech said:

Why is this site allowing such trash to be proliferated, and worse, documented? It’s an insult to those who have rigorously studied for years and spent tens of thousands of dollars to obtain credentials in science and engineering.

Click to expand...

The only true "perpetual" in PE is the never-ending effort to "prove" it works.

Milland said:

The only true "perpetual" in PE is the never-ending effort to "prove" it works.

Click to expand...

RC Mech said:

No please, do show your math. Charlatans omit the proof.

It’s a total waste of a biochem degree to even respond to this, but your chemical nomenclature makes no sense. They’re not even equations. Atmospheric chemistry is not “as easy as” that garbage you’ve posted.

Why is this site allowing such trash to be proliferated, and worse, documented? It’s an insult to those who have rigorously studied for years and spent tens of thousands of dollars to obtain credentials in science and engineering.

Click to expand...

And you just stated why no scientist would work cooperatively with me on my science experiment. They're successful. And if what I've
shown works, it was built over 300 years ago. If we consider engineering on its own merits, when a weight falls a distance of 40 inches,
can it lift a weight 10 inches? With the design I've shown, that is the question.
If you'd like, I can discuss the physics of why they say this isn't possible. They say a weight can't lift itself. The weight falling will be lifting
another weight.
A weight cannot lift another weight higher than itself. In the diagram shown, a weight dropping 40 inches will only lift another weight 10 inches.
And this has not been studied because it is not considered possible for a weight dropping 40 inches to lift another weight 10 inches. The
scientists who make these claims also said that powered flight is not possible and that it is not possible to exceed the speed of sound. Why
the Wright Bros. and Chuck Yeager made history. Basically a sonic boom or having no sound transmission would interfere with mechanics.

RC Mech said:

No please, do show your math. Charlatans omit the proof.

It’s a total waste of a biochem degree to even respond to this, but your chemical nomenclature makes no sense. They’re not even equations. Atmospheric chemistry is not “as easy as” that garbage you’ve posted.

Why is this site allowing such trash to be proliferated, and worse, documented? It’s an insult to those who have rigorously studied for years and spent tens of thousands of dollars to obtain credentials in science and engineering.

Click to expand...

Well, if he didn't keep changing the subject, he would soon run out of things to talk about...
Though, I gotta admit, I am curious to see where the energy to flip the dangling 'up-going' weights, is going to come from!

Must be somewhere in that math he understands so well...Who woulda ever thunk it all boiled down to a simple equation of 75% on one side, and 25% on the other? Physicists across the world must be ecstatic!

I'm personally pretty interested in knowing how a bearing with a bunch of (compounded friction) rolling elements is supposed to beat out the best that guys in the Labs at, say SKF, or FAG, (with actual measuring equipment) can come up with, let alone, why he thinks he can beat an air bearing for friction losses!

At best, I see him creating a collection of wooden models of PE machines that won't work. No problem with that, other than he thinks they will! I half expect to start hearing about Admiralty Law, and why the blocking of his 'Right to Travel', is what is holding his research back!

So far, I have not seen proof that they will even be all that well built models.

There is, some irony, in that he posts link to other sites, where they have pretty much sorted out who he is, and what his likely worth to the world at large is.

trevj said:

Well, if he didn't keep changing the subject, he would soon run out of things to talk about...
Though, I gotta admit, I am curious to see where the energy to flip the dangling 'up-going' weights, is going to come from!

Must be somewhere in that math he understands so well...Who woulda ever thunk it all boiled down to a simple equation of 75% on one side, and 25% on the other? Physicists across the world must be ecstatic!

I'm personally pretty interested in knowing how a bearing with a bunch of (compounded friction) rolling elements is supposed to beat out the best that guys in the Labs at, say SKF, or FAG, (with actual measuring equipment) can come up with, let alone, why he thinks he can beat an air bearing for friction losses!

At best, I see him creating a collection of wooden models of PE machines that won't work. No problem with that, other than he thinks they will! I half expect to start hearing about Admiralty Law, and why the blocking of his 'Right to Travel', is what is holding his research back!

So far, I have not seen proof that they will even be all that well built models.

There is, some irony, in that he posts link to other sites, where they have pretty much sorted out who he is, and what his likely worth to the world at large is.

Click to expand...

To answer your question, they never met me. Some scientists will like me. They will say plate tectonics, glacial melt allows for tectonic plates to rise,
thermal vents heat the ocean floor, deep faults heat the Arctic Ocean, etc. Not everyone says CO2.
It is a matter of ratios. 4:1 or 5:1 matters because of Gotta have sum fun, right?

This is HOT!!!!

Kind of my typical email. And you guys have no idea what this means. I'm being nice. I think I'll do some very nice woodworking and some science.
I need a life. That's my objective.

RC Mech said:

No please, do show your math. Charlatans omit the proof.

It’s a total waste of a biochem degree to even respond to this, but your chemical nomenclature makes no sense. They’re not even equations. Atmospheric chemistry is not “as easy as” that garbage you’ve posted.

Why is this site allowing such trash to be proliferated, and worse, documented? It’s an insult to those who have rigorously studied for years and spent tens of thousands of dollars to obtain credentials in science and engineering.

Click to expand...

The experiment I want to see tried will basically prove the IPCC wrong. And this will be using their own reports in 20001 and 2013. Who'd think a 300 year old
invention kept secret would create this problem? And this is because I'll be doing wood working without a shop. Who'd think it, right?

Clim said:

To answer your question, they never met me. Some scientists will like me. They will say plate tectonics, glacial melt allows for tectonic plates to rise,
thermal vents heat the ocean floor, deep faults heat the Arctic Ocean, etc. Not everyone says CO2.
It is a matter of ratios. 4:1 or 5:1 matters because of

Gotta have sum fun, right?

Click to expand...

Like I said. Keep's changing the subject!

Where's your math? Or squirrels?

trevj said:

Like I said. Keep's changing the subject!

Where's your math? Or squirrels?

Click to expand...

If you can't understand basic gear ratios, I can't win. Tomorrow for fun I will show the math. I will be using
analytical trigonometry. And then I'll show calculus. For this calculus doesn't get it. Then we can consider algebra
and trigonometry. Over the next couple of days we will discuss math.
With calculus, it shows rate of change. It relies on limits and surface area for determine the length of a line. You know, a curve
creates a surface area equal to the line. That's f(x) = dy/dx. I can and will do the math for you. And then we can know when
planing 2 boards, we'll be creating opposite surfaces to glue together. It's basically the same thing. Where I don't have a bench
for doing this. At the 11:15 mark, if 2 boards were clamped, they could be planed. Basic woodworking.

Clim said:

If you can't understand basic gear ratios, I can't win. Tomorrow for fun I will show the math. I will be using
analytical trigonometry. And then I'll show calculus. For this calculus doesn't get it. Then we can consider algebra
and trigonometry. Over the next couple of days we will discuss math.
With calculus, it shows rate of change. It relies on limits and surface area for determine the length of a line. You know, a curve
creates a surface area equal to the line. That's f(x) = dy/dx. I can and will do the math for you. And then we can know when
planing 2 boards, we'll be creating opposite surfaces to glue together. It's basically the same thing. Where I don't have a bench
for doing this. At the 11:15 mark, if 2 boards were clamped, they could be planed. Basic woodworking.

Click to expand...

Hope springs eternal, but I have my doubts that you can a.) Stay on subject, or b.) come up with anything that reasonably supports your theories!

Gear ratios are easy! Count teeth! Compare! But so far, that has had naught to do with what you propose!

But, thanks for the off-topic woodwork vid! An entertaining side trip from the topic at hand!